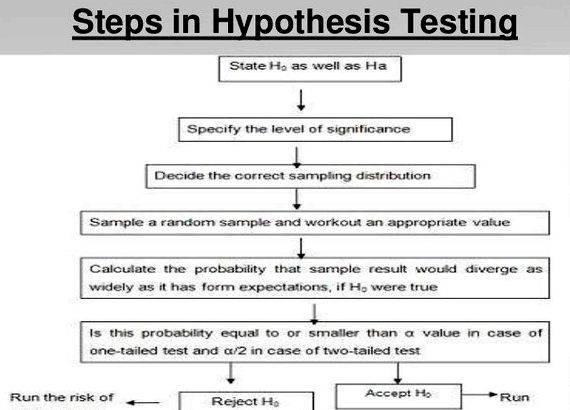
Steps in Statistical Hypothesis Testing

Step 1: State the null hypothesis, H0. and the alternative hypothesis, Ha. The alternative hypothesis represents what the researcher is trying to prove. The null hypothesis represents the negation of what the researcher is trying to prove. (In a criminal trial in the American justice system, the null hypothesis is that the defendant is innocent; the alternative is that the defendant is guilty; either the jury rejects the null hypothesis if they find that the prosecution has presented convincing evidence, or the jury fails to reject the null hypothesis if they find that the prosecution has not presented convincing evidence).

Step 2: State the size(s) of the sample(s). This represents the amount of evidence that is being used to make a decision. State the significance level. a. for the test. � The significance level is the probability of making a Type I error. A Type I error is a decision in favor of the alternative hypothesis when, in fact, the null hypothesis is true. A Type II error is a decision to fail to reject the null hypothesis when, in fact, the null hypothesis is false.

Step 3: State the test statistic that will be used to conduct the hypothesis test (the appropriate test statistics for the different kinds of hypothesis tests are given in the tables of the reference page, �Statistical Inference for Values of Population Parameters�). The following statement should appear in this step: �The test statistic is ________ _. which under H0 has a _____________ probability distribution (with _____ degrees of freedom).� �

Step 4: Find the critical value for the test. This value represents the cutoff point for the test statistic. If the null hypothesis were true, there would be only a probability of a of obtaining a value of the test statistic that would be at least this extreme.

If the value of the test statistic computed from the sample data is beyond the critical value, the decision will be made to reject the null hypothesis in favor of the alternative hypothesis.

Step 5: Calculate the value of the test statistic, using the sample data. (If you are using Excel or SAS, or some similar computer package, you will calculate the value of the test statistic, along with a p-value.)

Step 6: Decide. based on a comparison of the calculated value of the test statistic and the critical value of the test, whether to reject the null hypothesis in favor of the alternative. (If you have a calculated p-value, then decide based on a comparison of the p-value with a. If the p-value is less than a. reject H0. Otherwise, fail to reject H0 .)

If the decision is to reject H0. the statement of the conclusion should read as follows: �We reject H0 at the (value of a ) level of significance. There is sufficient evidence to conclude that (statement of the alternative hypothesis).�

If the decision is to fail to reject H0. the statement of the conclusion should read as follows: �We fail to reject H0 at the (value of a ) level of significance. There is not sufficient evidence to conclude that (statement of the alternative hypothesis).�

Steps in Statistical Hypothesis Testing

Step 1: State the null hypothesis, H0. and the alternative hypothesis, Ha.

The alternative hypothesis represents what the researcher is trying to prove. The null hypothesis represents the negation of what the researcher is trying to prove. (In a criminal trial in the American justice system, the null hypothesis is that the defendant is innocent; the alternative is that the defendant is guilty; either the jury rejects the null hypothesis if they find that the prosecution has presented convincing evidence, or the jury fails to reject the null hypothesis if they find that the prosecution has not presented convincing evidence).

Step 2: State the size(s) of the sample(s). This represents the amount of evidence that is being used to make a decision. State the significance level. a. for the test. � The significance level is the probability of making a Type I error. A Type I error is a decision in favor of the alternative hypothesis when, in fact, the null hypothesis is true. A Type II error is a decision to fail to reject the null hypothesis when, in fact, the null hypothesis is false.

Step 3: State the test statistic that will be used to conduct the hypothesis test (the appropriate test statistics for the different kinds of hypothesis tests are given in the tables of the reference page, �Statistical Inference for Values of Population Parameters�). The following statement should appear in this step: �The test statistic is ________ _. which under H0 has a _____________ probability distribution (with _____ degrees of freedom).� �

Step 4: Find the critical value for the test. This value represents the cutoff point for the test statistic. If the null hypothesis were true, there would be only a probability of a of obtaining a value of the test statistic that would be at least this extreme. If the value of the test statistic computed from the sample data is beyond the critical value, the decision will be made to reject the null hypothesis in favor of the alternative hypothesis.

Step 5: Calculate the value of the test statistic, using the sample data. (If you are using Excel or SAS, or some similar computer package, you will calculate the value of the test statistic, along with a p-value.)

Step 6: Decide. based on a comparison of the calculated value of the test statistic and the critical value of the test, whether to reject the null hypothesis in favor of the alternative. (If you have a calculated p-value, then decide based on a comparison of the p-value with a. If the p-value is less than a. reject H0. Otherwise, fail to reject H0 .)

If the decision is to reject H0. the statement of the conclusion should read as follows: �We reject H0 at the (value of a ) level of significance. There is sufficient evidence to conclude that (statement of the alternative hypothesis).�

If the decision is to fail to reject H0. the statement of the conclusion should read as follows: �We fail to reject H0 at the (value of a ) level of significance. There is not sufficient evidence to conclude that (statement of the alternative hypothesis).�