Because of constant downscaling of gate-dielectric thicknesses in modern MOS devices the result of tunneling has drastically acquired relevance. Quantum mechanical tunneling describes the transition of carriers via a classically forbidden energy condition. This is often an electron tunneling in the semiconductor via a dielectric, addressing a power barrier, towards the gate contact of the MOS structure. Whether or not the energy barrier is greater compared to electron energy, there’s quantum robotically a finite possibility of this transition. The main reason is based on the wavelike behavior of particles around the quantum scale in which the wave function describes the prospect of finding an electron in a certain position wide. Because the wave function penetrates the barrier and may even extend to another side, quantum mechanics predict a non-zero probability to have an electron to become on the other hand.
Figure 5.4 depicts the power band diagrams for 2 tunneling mechanisms within an MOS structure composed of the p-type bulk plastic, dielectric, along with a n polycrystalline plastic gate.
In Figure 5.4(a) the power band conditions for that direct tunneling regime are proven. Here, the electrons in the inverted plastic surface can tunnel directly with the forbidden energy barrier created through the dielectric layer towards the poly-gate. Direct tunneling is strongly gaining significance once the dielectric layer will get thinner.
A typical method of model the tunneling current may be the Tsu-Esaki formula [67 ]
where may be the electron mass in plastic and also the electron mass within the dielectric [68 ]. may be the transmission coefficient and also the supply function that is given as
Here, and denote the power distribution functions close to the interfaces [69 ].
The power band conditions for Fowler-Nordheim tunneling, that is a special situation of direct tunneling, are portrayed in Figure 5.4(b). The electrons don’t tunnel directly to another side from the barrier. Rather they tunnel in the plastic inversion layer towards the conduction gang of the layer where they’re transported towards the gate contact. The Fowler-Nordheim regime is important for thicker dielectrics and sufficiently high electric fields.
An intensive analysis of modeling and simulation of tunneling mechanisms are available in the thesis of Gehring [69 ].
5.3.2 Trap-Aided Tunneling
Because the decrease in the applied voltages doesn’t take care of the miniaturization of actual devices the electrical fields across dielectric layers are continually growing. Specifically for non-volatile memory cells high electric fields are essential to have quick write and erase cycles. Because of the repeated high-field stress, defects can arise within the dielectric resulting in tunneling currents, even at low fields. This stress-caused leakage current (SILC) [70 ,71 ] plays a significant role within the resolution of the retention occasions of non-volatile memory cells.
There are lots of methods to model trap-aided tunneling (TAT). The first is to model the defect aided tunneling process together with a single trap. For every trap position tunneling in the cathode towards the trap and additional towards the anode is recognized as. Out of this the trap occupancy function could be calculated which is often used to compute the tunneling current [72 ].

This single-TAT approach is effective for slightly degraded devices or devices with thin gate dielectrics. For thicker dielectrics having a high defect density it’s reasonable to visualize which the interaction of several traps within the tunneling process happens [73 ].
For that modeling of multi-trap aided tunneling (multi-TAT) approaches just like a two-trap process [74 ,75 ] or perhaps a multi-trap process thinking about hopping of carriers between distinct defects [76 ] happen to be presented. Lately, anomalous charge reduction in floating-gate memory cells continues to be reported [73 ], in which a two-trap model was utilized to breed the measured data.
For proper modeling of these highly degraded devices a brand new approach is suggested included in the work. It rigorously computes TAT current aided by multiple traps [77 ,78 ]. Within this model hopping processes between all oxide defects are taken into consideration. Additionally the filling of oxide traps with carriers, resulting in space charge within the oxide and for that reason to some shift from the threshold current, is taken into account. This shift can result in circuit failure because the timing parameters from the device are degraded.
The model for that simulation of SILC in highly degraded devices is dependant on inelastic, phonon-aided tunneling [79 ] using the tunneling-rate suggested by Herrmann and Schenk [72 ]. These approaches are extended for modeling the interaction of multiple traps within the tunneling process.
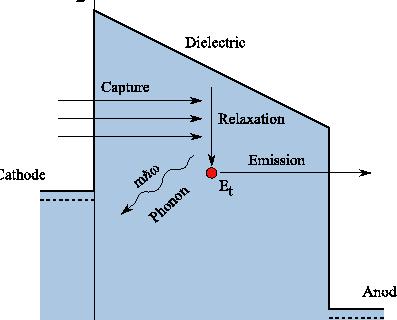
Figure 5.5: Inelastic tunneling process together with a sole trap. The surplus energy from the tunneling electron is released by way of phonon emission.
The defect-aided tunneling procedure for an electron in the cathode towards the anode using a trap is recognized as a 2-step process. Electrons are taken in the cathode, relax towards the degree of energy from the trap by emitting a number of phonons using the energy , and therefore are then released towards the anode. This method is inelastic because the electron energy isn’t conserved throughout the tunneling process. Figure 5.5 depicts this method such as the phonon emission.
Within the single-trap aided tunneling approach the tunneling current for every trap is calculated individually. The entire tunneling current is later on superimposed in the individual contributions. Even though the interaction between neighboring traps is worth focusing on in highly degraded dielectrics (Section 5.3.2.3 ), at a lower price degraded devices this method may be used [72 ,80 ].
The tunneling current density is modeled as the sum of the capture or emission rates of every trap, or , that are equal within the stationary situation, , multiplied through the trap mix section ,
The summation index gives the amount of discrete phonon emissions, may be the phonon energy, and may be the multiphonon transition probability [72 ]. The symbols and represent the Fermi-distributions, the electrical field within the dielectric, and also the band gap of . The transmission coefficients were evaluated with a statistical WKB method which yields reasonable precision for single-layer dielectrics. This model has been utilized inside a pretty much similar form by various authors [80 ,79 ,82 ].
Figure 5.6: Multi-trap aided tunneling process. The tunneling rate of the specific trap is dependent upon all capture and emission occasions back and forth from the trap.
5.3.2.3 Multi-Trap Aided Tunneling
For highly degraded devices the isolated calculation for every trap isn’t sufficient any longer [74 ]. Anomalous charge reduction in memory cells continues to be observed and it was described by conduction via a second trap [74 ]. The only-trap model could be extended with this situation, and also the rate equations become (see Figure 5.6 )
An average quantity of unknowns from the equation product is 15. With respect to the dielectric thickness and trap energy the end result doesn’t improve when further growing the dpi. The computational effort remains minimal when compared to total device simulation time. The multi-trap aided tunneling current density may then be acquired in the capture or emission rates
By coupling this model towards the semiconductor device equations (Section 2.1 ) the simulation from the aftereffect of billed defects around the threshold current of memory devices can be done. The area charge density within the dielectric is calculated in the trap occupation work as





 Neon genesis evangelion angels thesis proposal
Neon genesis evangelion angels thesis proposal Sample thesis proposal for business administration
Sample thesis proposal for business administration Haruko obokata phd thesis proposal
Haruko obokata phd thesis proposal University of the philippines list of thesis proposal
University of the philippines list of thesis proposal Lse gender institute dissertation proposal
Lse gender institute dissertation proposal






