In chapter 2 we outline some of the founding principles of quantum mechanics, highlighting the origin of the complexity of the problem of quantum-mechanical many-body systems, describing how the electronic and nuclear degrees of freedom can be separated and demonstrating the power of variational methods for solving the quantum-mechanical equations.
In chapter 3 we turn to a description of the problem of the inhomogeneous “gas” of interacting electrons moving in a static potential due to the nuclei. Density-functional theory allows us to tackle the many-body problem and obtain all of the ground-state properties of the electronic system. We outline in particular the local density approximation for exchange and correlation, the treatment of periodic systems and the pseudopotential approximation. The latter allows the calculation to be simplified by eliminating the chemically inert core electrons from the simulation.
In chapter 4 we generalise DFT to include partial occupation of single-particle states. From this the density-matrix formulation of density-functional theory can be derived, and we show how this can be used to obtain a foundation for linear-scaling methods. We discuss the various requirements this makes on the form of the density-matrix, and also the constraints which must be applied to obtain physically meaningful solutions, focusing in particular on the difficult idempotency condition. We also consider some of the issues which arise when the density-matrix is expressed in terms of a set of non-orthogonal functions.
In chapter 5 we address one of the issues raised by preliminary investigations: how to describe the density-matrix in real-space and still deal accurately with quantities naturally treated in reciprocal-space, particularly the kinetic energy.
We propose a new set of localised basis functions, for which analytic results for the overlap, kinetic energy and non-local pseudopotential matrix elements can be obtained, thus satisfying the demand to concentrate on a real-space description while still evaluating these quantities accurately.
In chapter 6 we discuss the use of penalty functionals to impose the idempotency constraint. We begin by reviewing Kohn’s proposal for the use of a penalty functional to exactly impose the idempotency constraint, and show how this is incompatible with computational minimisation schemes. We then present an original method which uses a penalty functional to approximately impose the idempotency constraint, but which still allows the use of efficient minimisation algorithms. Because the density-matrix obtained by this method is only approximately idempotent, the total energy calculated from it differs from the true ground-state energy. We therefore show how it is possible to derive a correction to the total energy from the penalty functional, which gives very accurate estimates of the true ground-state energy from only approximately idempotent density-matrices.
In chapter 7 we outline how the scheme of chapter 6 can be implemented computationally, focusing first on the calculation of the energy and its derivatives. We then examine these derivatives to show that the two types of variation which are made are equivalent to solving the Kohn-Sham equations and making the Hamiltonian and density-matrix commute.
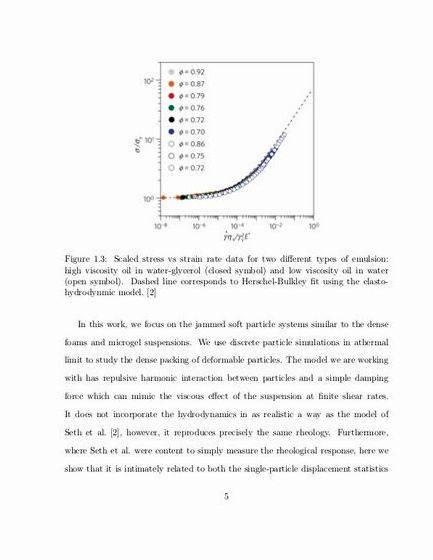
We describe how the gradients may be improved by preconditioning, and also how they should be corrected to take account of their tensor properties. Finally we discuss the imposition of the normalisation constraint, and give a general outline of the scheme as currently implemented.
In chapter 8 we describe methods for relating the different quantities used in traditional and linear-scaling calculations and show how the results obtained from one method can be used in the other. We concentrate on the application of such methods to obtain good initial density-matrices for linear-scaling calculations which can speed up the convergence to the ground-state solution.
In chapter 9 we present results for the scheme outlined in chapters 6 and 7 when applied to bulk crystalline silicon. We show how the energy converges as the range of the density-matrix is increased, and compare predicted physical properties with those calculated using traditional methods and with experiment. We also consider the scaling of the method with respect to system-size and the density-matrix range.




 Thesis writing guidelines ppt airport
Thesis writing guidelines ppt airport 1984 government control thesis proposal
1984 government control thesis proposal Record management system thesis introduction writing
Record management system thesis introduction writing Macroeconomics topics for thesis writing
Macroeconomics topics for thesis writing Textual presentation in thesis writing
Textual presentation in thesis writing