Inside my system I’m capable of write lower the Hamiltonian during this form:
$$ H = begin epsilon_-mu_B epsilon_+mu_B epsilon_+mu_B epsilon_-mu_B finish $$
where $mu_B$ would be the Zeeman split.
Now If perhaps to produce this process in touch with a superconductor and also write lower the Bogoliubov – de Gennes Hamiltonian. Personally the Bogoluibov – de Gennes Hamiltonian has this sort because the Zeeman energy doesn’t dependent which i have quasiparticle or holes:
$$ mathcal = begin epsilon_ epsilon_ epsilon_ epsilon_ endtau_ + begin -mu_B +mu_B +mu_B -mu_B end1_ + H_tau_ $$
Without Zeeman term the issue is a typical textbook problem, since i have have have have directly my Nambu spinor $psi^ = left(c^_,c^_,c^_,c^_,c_,c_,c_,c_right)$ and may write lower the Hamiltonian within the correct second quantization notation.
However, if Then i add Zeeman energy within my second quantization Hamiltonian vanish my Zeeman term by using this Nambu spinor. In situation your write within my Bogoliubov – de Gennes
$$ begin -mu_B +mu_B +mu_B -mu_B endtau_ $$
I choose the right results but meaning I have had a sign switch within my Bogoliubov – de Gennes Hamiltonian for quasiparticles an holes, that’s personally wrong!
My question now’s generate earnings must changes my Nambu spinor to make certain that my Zeeman term within my Hamiltonian can perform not vanish or can I’ve had an indication switch for quasiparticles and holes within the Zeeman energy?
The very best is clearly to begin within the normal type of the Hamiltonian, in your situation similar to $$Hsim c^left(dfrac>-mu+hsigma_right)c+Delta c^c^+Delta^cc$$ and to reproduce the de Gennes calculation. A few in the details exist: physics.stackexchange.com/questions/77298 The factor is — by having an unknown reason — teacher tell for that students the Bogoliubov-deGennes Hamiltonian describes superconductivity. This is often just wrong, the mean-field Hamiltonian I authored above will it, the BdG is just a formal rewriting out of this. FraSchelle Marly 5 ’14 at 8:54
Note in addition the Nambu spinor is 2 occasions too big. Since particle and holes are coupled within the BdG description, your $c_$ notation appears redundant personally. Consider also giving us your detailed solution, assistance others obtaining the identical problem. Your previous comment is just wrong: the BdG representation needs both matrix and the vector to obtain defined. Particle-hole symmetry means nothing have you been to supply us just the matrix. Enjoy yourself. FraSchelle Marly 5 ’14 at 9:00
No, Nambu spinor is true. I think about the closeness-caused effect in Carbon nanotubes along with the 1 and 2 means the various valleys. Personally the solution is, once i perform transformation from particle to hole and the opposite way round than this doesn’t modify the spin within the particle/hole. Means particle-hole transformation preserved the spin.
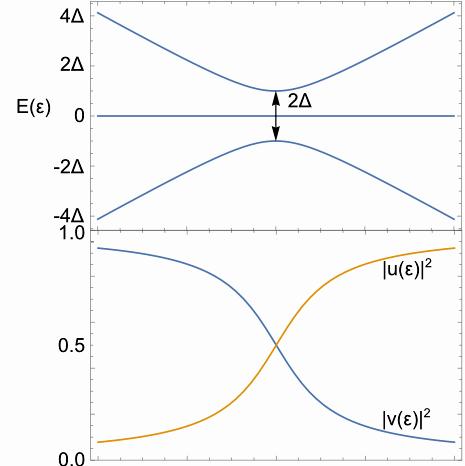
Once the Zeeman splitting shift the particle energy lower must then for the hole the Zeeman splitting must shift the power up. I’m wishing this is often apparent. user27964 Marly 5 ’14 at 17:59
Inside my system I’m capable of write lower the Hamiltonian during this form:
$$ H = begin epsilon_-mu_B epsilon_+mu_B epsilon_+mu_B epsilon_-mu_B finish $$
where $mu_B$ would be the Zeeman split.
Now If perhaps to produce this process in touch with a superconductor and also write lower the Bogoliubov – de Gennes Hamiltonian. Personally the Bogoluibov – de Gennes Hamiltonian has this sort because the Zeeman energy doesn’t dependent which i have quasiparticle or holes:
$$ mathcal = begin epsilon_ epsilon_ epsilon_ epsilon_ endtau_ + begin -mu_B +mu_B +mu_B -mu_B end1_ + H_tau_ $$
Without Zeeman term the issue is a typical textbook problem, since i have have have have directly my Nambu spinor $psi^ = left(c^_,c^_,c^_,c^_,c_,c_,c_,c_right)$ and may write lower the Hamiltonian within the correct second quantization notation.
However, if Then i add Zeeman energy within my second quantization Hamiltonian vanish my Zeeman term by using this Nambu spinor. In situation your write within my Bogoliubov – de Gennes
$$ begin -mu_B +mu_B +mu_B -mu_B endtau_ $$
I choose the right results but meaning I have had a sign switch within my Bogoliubov – de Gennes Hamiltonian for quasiparticles an holes, that’s personally wrong!
My question now’s generate earnings must changes my Nambu spinor to make certain that my Zeeman term within my Hamiltonian can perform not vanish or can I’ve had an indication switch for quasiparticles and holes within the Zeeman energy?
The very best is clearly to begin within the normal type of the Hamiltonian, in your situation similar to $$Hsim c^left(dfrac>-mu+hsigma_right)c+Delta c^c^+Delta^cc$$ and to reproduce the de Gennes calculation. A few in the details exist: physics.stackexchange.com/questions/77298 The factor is — by having an unknown reason — teacher tell for that students the Bogoliubov-deGennes Hamiltonian describes superconductivity. This is often just wrong, the mean-field Hamiltonian I authored above will it, the BdG is just a formal rewriting out of this. FraSchelle Marly 5 ’14 at 8:54
Note in addition the Nambu spinor is 2 occasions too big. Since particle and holes are coupled within the BdG description, your $c_$ notation appears redundant personally. Consider also giving us your detailed solution, assistance others obtaining the identical problem. Your previous comment is just wrong: the BdG representation needs both matrix and the vector to obtain defined. Particle-hole symmetry means nothing have you been to supply us just the matrix. Enjoy yourself. FraSchelle Marly 5 ’14 at 9:00
No, Nambu spinor is true. I think about the closeness-caused effect in Carbon nanotubes along with the 1 and 2 means the various valleys. Personally the solution is, once i perform transformation from particle to hole and the opposite way round than this doesn’t modify the spin within the particle/hole. Means particle-hole transformation preserved the spin. Once the Zeeman splitting shift the particle energy lower must then for the hole the Zeeman splitting must shift the power up. I’m wishing this is often apparent. user27964 Marly 5 ’14 at 17:59
Writing master s thesis tips to winning
Brian may astrophysicist thesis writing
Moi university thesis writing guidelines
Scientific topics for thesis writing
Writing your thesis oliver patrick
